Contente

• Passos
• Método 1 de 3: Parte 1: Determinando o Ponto de Inflexão
• Método 2 de 3: Calculando os derivados de uma função
• Método 3 de 3: Parte 3: Encontre o Ponto de Inflexão
• Pontas

No cálculo diferencial, um ponto de inflexão é um ponto em uma curva no qual sua curvatura muda de sinal (de mais para menos ou de menos para mais). Este conceito é usado em engenharia mecânica, economia e estatística para identificar mudanças significativas nos dados.

Passos

Método 1 de 3: Parte 1: Determinando o Ponto de Inflexão

1. 1 Definição de função côncava. O meio de qualquer acorde (um segmento conectando dois pontos) do gráfico de uma função côncava fica sob o gráfico ou sobre ele.
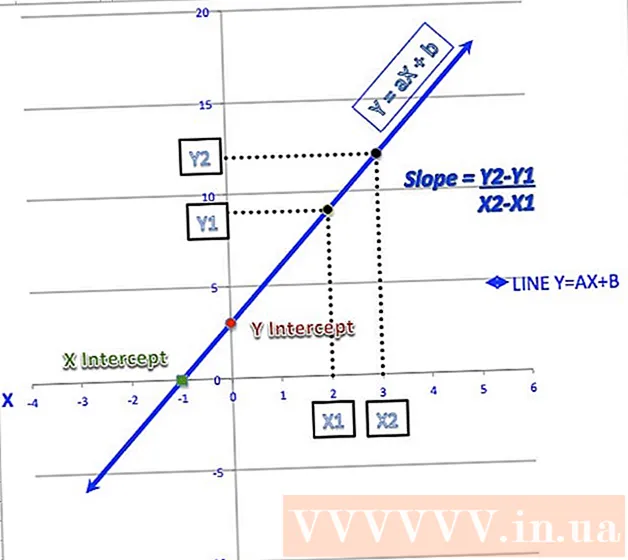
2. 2 Definição de função convexa. O meio de qualquer acorde (um segmento conectando dois pontos) do gráfico de uma função convexa fica acima do gráfico ou sobre ele.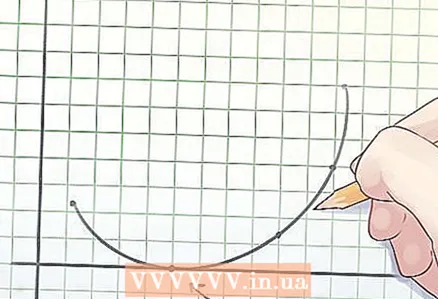
3. 3 Determinação das raízes da função. A raiz de uma função é o valor da variável "x" em que y = 0.
   • Ao plotar uma função, as raízes são os pontos nos quais o gráfico cruza o eixo x.

Método 2 de 3: Calculando os derivados de uma função

1. 1 Encontre a primeira derivada da função. Observe as regras de diferenciação no livro didático; você tem que aprender como tirar as primeiras derivadas e só então passar para cálculos mais complexos. As primeiras derivadas são designadas f '(x). Para expressões da forma ax ^ p + bx ^ (p - 1) + cx + d, a primeira derivada é: apx ^ (p - 1) + b (p - 1) x ^ (p - 2) + c.
   • Por exemplo, encontre os pontos de inflexão da função f (x) = x ^ 3 + 2x -1. A primeira derivada desta função é:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Encontre a segunda derivada da função. A segunda derivada é a derivada da primeira derivada da função original. A segunda derivada é denotada como f ′ ′ (x).
   • No exemplo acima, a segunda derivada é:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Defina a segunda derivada como zero e resolva a equação resultante. O resultado será o ponto de inflexão esperado.
   • No exemplo acima, seu cálculo é semelhante a este:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Encontre a terceira derivada da função. Para verificar se o seu resultado é realmente um ponto de inflexão, encontre a terceira derivada, que é a derivada da segunda derivada da função original. A terceira derivada é denotada como f ′ ′ ′ (x).
   • No exemplo acima, a terceira derivada é:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Método 3 de 3: Parte 3: Encontre o Ponto de Inflexão

1. 1 Confira a terceira derivada. A regra padrão para estimar um ponto de inflexão é que se a terceira derivada não for zero (ou seja, f ′ ′ ′ (x) ≠ 0), então o ponto de inflexão é o verdadeiro ponto de inflexão. Confira a terceira derivada; se não for zero, você encontrou o ponto de inflexão real.
   • No exemplo acima, a terceira derivada é 6, não 0.Então você encontrou o verdadeiro ponto de inflexão.
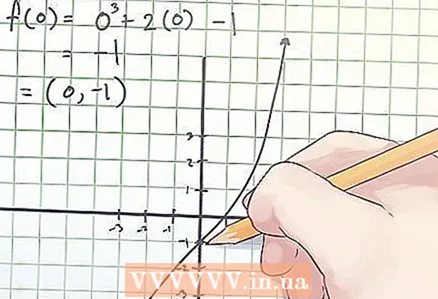
2. 2 Encontre as coordenadas do ponto de inflexão. As coordenadas do ponto de inflexão são denotadas como (x, f (x)), onde x é o valor da variável independente "x" no ponto de inflexão, f (x) é o valor da variável dependente "y" na inflexão apontar.
   • No exemplo acima, ao igualar a segunda derivada a zero, você descobriu que x = 0. Portanto, para determinar as coordenadas do ponto de inflexão, encontre f (0). Seu cálculo é assim:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
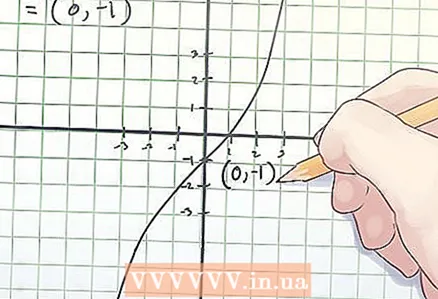3. 3 Anote as coordenadas do ponto de inflexão. As coordenadas do ponto de inflexão são os valores encontrados de x e f (x).
   • No exemplo acima, o ponto de inflexão está nas coordenadas (0, -1).

Pontas

• A primeira derivada de um termo livre (número primo) é sempre zero.